指揮者でもある数学教師が語る『数学と音楽の共通点』（その２～音楽の論理≒和声進行の基礎）

前回の記事（その１）で数学と音楽には論理を読み解くという点で共通点がある、と書きました。そして音楽の「論理」はハーモニー（和声）にあることも書きました。

そこで、今回は和声進行のの論理について、その基礎となる部分を書きたいと思います。

和音と和音記号

まずは和音と和音記号を学びましょう

下の楽譜はハ長調とハ短調の和音と和音記号です（出典：wikipedia）

和音の機能

和音には機能（役割）があります。

特に重要なのが、トニカ（T）とドミナント（D）とサブドミナント（S）の３つの和音です。それぞれの機能については、wikipediaの説明がよくまとまっていますので、譜例と共に引用させていただきます。

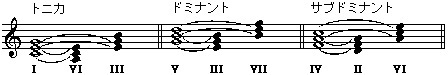
《トニカ（T）》

和声の中心となる機能である。この和音が鳴らされるとき、「落ち着き」「解放」「解決」「弛緩」といった印象を与える。「自宅」のイメージである。楽曲の最後はトニカで終わる。 I のほか、 VI も I の代理の時、トニカの機能を持つ（ドミナントから VI に終止する終止形は偽終止という）。 III もトニカの機能を持つことがある。

注）代理（和音）とは、ある和音の代わりに使われる和音で、似た響きを持ち、ほぼ同じ機能を持つ和音のことである。（中略）

《ドミナント（D）》

トニカの5度上の和音であり、トニカとは対照的に、「緊張」した印象を与える。「外出先」のイメージである。トニカに移行しようとする力が強い（トニカに移行するように緊張が解ける方向で移行することを解決と呼ぶ）。 V に第7音を加えて V7の和音で現れることが多く、 V9の和音もよく用いられる。また、 III や VII も V の代理の時、ドミナントの機能を持つ。

《サブドミナント（S）》

トニカの4度上、すなわち5度下の和音である。ドミナントほど強くないが、トニカに比べれば「緊張」した印象を与える。「発展」「外向的」な印象が強い。ドミナントに移行するか、トニカに解決する。 II や II7は、 IV とともに非常によく使われるサブドミナントである（ただし、 II はトニカには移行しない）。また、 VI が IV の代理和音としてサブドミナントの機能を持つことがある。（後略）

和声進行の基礎（カデンツ）

ここで、和声進行の基礎であるカデンツというものを紹介します。

カデンツとは

・T→D→T

・T→S→D→T

・T→S→T

のいずれかの和声進行のことを言います。この中で皆さんに一番馴染みがあるのはきっとT→S→D→Tの進行だと思います。なぜならこれは、音楽の授業の時の

「起り～つ（T）→気をつけ～（S）→礼～（D）→なおれ～（T）」

の進行だからです。

で、ここからが重要なところですが、D（礼）の和音に入る前に音楽が止まってしまうと、とても不自然な感じがする、ということです。誰でも「気をつけ～」で間延びすると早く「礼」になって欲しいと感じるはずです。

しかし不思議なことに、一度D（礼）に入ってしまうと、今度は少々その時間が長くなっても不自然には感じません。腰のあたりが痛くなってくるという身体的な不都合はあるかもしれませんが（笑）、音楽的には例えば、D（礼）の長さが、S（気をつけ～）の２倍あったとしても、ほとんど違和感を感じないと思います。逆にD（礼）の長さがS（気をつけ）より短くなってしまうと、何か勿体無いような、先生をバカにしているかのような奇妙な感じを受けると思います。

ただ、D（礼）の時間が長くなってもいいと言っても、このD（礼）の和音が鳴っている間は心情的に緊張感が続いています。そこがミソです。そして、その緊張の後にT（なおれ）が来ると、ホッとします。それは、「ああ、戻った～」という安堵感、喜びがあって、緊張が緩和するからです。

つまり、聴いていて気持の良い音楽を作るためには、Dの和音に入る前は音楽を進め、Dの和音に入ったら慌てずに自然とTに着地できるだけの時間を取る、という風にカデンツを作ることが必要になります。極言すれば、音楽を演奏するというのは、カデンツにおいて緊張→緩和の自然な流れを作ることだ、と私は思います。

以上のことは、多分に単純化して書いています。実際の曲は、例えそれが古典派の曲であっても、簡単にはDが見つからない場合もあります。作曲家は色々な形で曲の中でDを作るからです。もちろん一番基本的なⅤやⅤ7の和音で表れることも少なくありませんが、代理の和音で表れたり、三全音などの省略された形で表れたり、和音ではなく転調で作るDやリズムで作るDなどもあって、なかなか一筋縄ではいきません。

だからこそ、指揮者の勉強の最大の目的は、その様々なDをスコアの中に見つけ、作曲家が望んだカデンツを作ることだと私は思っています。

いかがでしょうか？音楽が非常に論理的に構築されていることがお分かりいただけましたでしょうか？私達がスコアを読む目的の大半はこの論理を発見することです。音楽において（和声の）辻褄が合うことを確認しようとする頭のはたらきは、数学において数式を読むときのそれと非常に似通っています。

次回は数学者と音楽、あるいは音楽家と数学について書きたいと思います。